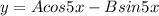Answer:
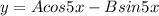
Explanation:
Given the differential equation y''-10y'+29y=0
First, we need to rewrite it as an auxiliary equation as shown:
Let y'' = m²y and y' = my
Substitute the values into the general equation
m²y-10my+29y = 0
Factor out y:
(m²-10m+29)y = 0 [The auxiliary equation]
Solve the auxiliary equation and find the roots of the equation
m²-10m+29 = 0
m = -b±√(b²-4ac)/2a
a = 1, b = -10, c = 29
m = -10±√(10²-4(1)(29))/2(1)
m = -10±√(100-116)/2
m = -10±√-16/2
m = (-10±4i)/2
m = -10/2 + 4i/2
m = -5+2i
Comparing the complex number with a+bi, a = -5 and b = 2
The general solution for complex solution is expressed as:
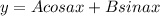
Substitute the value of a in the equation
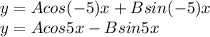
Hence the general solution to the differential equation is