Question

You measure the period of a mass oscillating on a vertical spring ten times as follows:

Period (s): 1.06, 1.31, 1.28, 0.99, 1.48, 1.37, 0.98, 1.31, 1.59, 1.55

Required:
What are the mean and (sample) standard deviation?

a. Mean: 1.228, Standard Deviation: 0.2135
b. Mean: 1.325, Standard Deviation: 0.1674
c. Mean: 1.292. Standard Deviation: 0.2211
d. Mean: 1.228, Standard Deviation: 0.2098
e. Mean: 1.292, Standard Deviation: 0.2135

Answer 1

Explanation:

Mean is the ratio of sum of the dataset to the sample size. Mathematically:

`\overline x = (\sum Xi)/(N)`

Xi are the individual periods

N is the sample size

`\sum Xi = 1.06+1.31+1.28+0.99+1.48+1.37+0.98+1.31+1.59+1.55\\\sum Xi = 12.92`

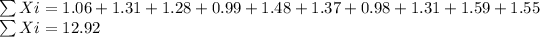
N = 10

Substitute

`\overline x = (12.92)/(10)\\\overline x = 1.292`

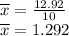
hence the mean of the samples is 1.292

For the standard deviation:

`\sigma = \sqrt{(\sum (x-\overline x)^2)/(N) } \\`

`\sum (x-\overline x)^2 = (1.06-1.292)^2+ (1.31-1.292)^2+ (1.28-1.292)^2+ (10.99-1.292)^2+ (1.48-1.292)^2+ (1.37-1.292)^2+ (0.98-1.292)^2+ (1.31-1.292)^2+ (1.59-1.292)^2+ (1.55-1.292)^2\\\sum (x-\overline x)^2 = 0.43996`

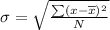
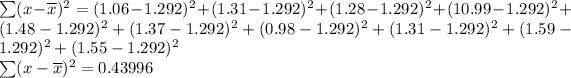
Substitute into the formula:

`\sigma = \sqrt{(0.43996)/(10) }} \\\sigma = \sqrt{{0.043996}}} \\\sigma = 0.2098`

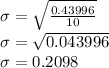
Hence the standard deviation is 0.2098