Answer:
a
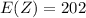
b
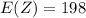
c

Explanation:
From the question we are told that
The mean of X is
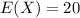
The standard deviation of X is
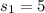
The mean of Y is
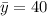
The standard deviation of Y is
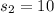
Considering question a
Generally the mean of Z = 2 + 10X. is mathematically represented
![E(Z) = E[2 + 10X ]](https://img.qammunity.org/2021/formulas/mathematics/college/a92m49zewza0kvwb14fldr2dopzsyhdcwr.png)
=>

=>
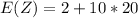
=>
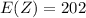
Considering question b
Generally the mean of Z = 10X - 2.. is mathematically represented
![E(Z) = E[10X -2 ]](https://img.qammunity.org/2021/formulas/mathematics/college/3ci9ui8a2yijv7c278d9cdg7692t3chdky.png)
=>
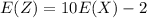
=>

=>
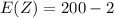
=>
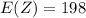
Considering question c
Generally the mean of -3X - 2Y is mathematically represented
![E(Z) = E[-3X -2Y ]](https://img.qammunity.org/2021/formulas/mathematics/college/vmivpfhfo0frlcv3gp7ophvgjtaymreezv.png)
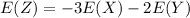
=>
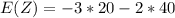
=>
