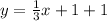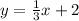Question

LaTeX: Create\:an\:equation\:in\:slope\:intercept\:form\:that\:is\:parallel\:to\:y\:=\frac{\:1}{3}x\:+\:4\:and\:goes\:through\:the\:point\:\left(-3,\:1\right).C r e a t e a n e q u a t i o n i n s l o p e i n t e r c e p t f o r m t h a t i s p a r a l l e l t o y = 1 3 x + 4 a n d g o e s t h r o u g h t h e p o i n t ( − 3 , 1 ) .

Group of answer choices


LaTeX: y=\frac{1}{3}x+2 y = 1 3 x + 2 y = 1 3 x + 2 y = 1 3 x + 2


LaTeX: y\:=\:-3x\:+\:4 y = − 3 x + 4 y = − 3 x + 4 y = − 3 x + 4


LaTeX: y=\frac{1}{3}x y = 1 3 x y = 1 3 x y = 1 3 x


LaTeX: y=-3x-8

Answer 1

`y = (1)/(3)x +2`

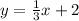
Explanation:

Given

Equation:

`y = (1)/(3)x + 4`

`Point: (-3,1)`

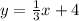
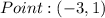
Required

Determine the equation of the point parallel to the given equation

First, we need to determine the slope of:
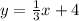`y = (1)/(3)x + 4` using

`y = mx + b`

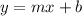
Where m represents slope.

By comparison

`m = (1)/(3)`

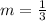
The equation of the point is calculated as thus:

`y - y_1 = m(x - x_1)`

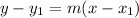
Where
`(x_1,y_1) = (-3,1)`

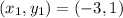
So, we have:

`y - y_1 = m(x - x_1)`

`y - 1 = (1)/(3)(x - (-3))`

`y - 1 = (1)/(3)(x +3)`

`y - 1 = (1)/(3)x +1`

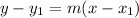
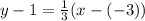
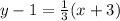
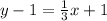
Solve for y

`y = (1)/(3)x +1 +1`

`y = (1)/(3)x +2`