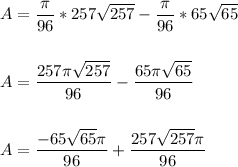Question

How do you do this question?

Answer 1

Part 1

`x = g(y), \ c \le y \le d\\\\\\x = 3+4y^2, \ 1 \le y \le 2\\\\\\(dx)/(dy) = 8y, \ 1 \le y \le 2\\\\\\\displaystyle A = 2\pi \int_(c)^(d)y√(1+[g'(y)]^2)dy\\\\\\\displaystyle A = 2\pi \int_(c)^(d)y\sqrt{1+\left[(dx)/(dy)\right]^2}dy\\\\\\\displaystyle A = 2\pi \int_(1)^(2)y√(1+(8y)^2)dy\\\\\\\displaystyle A = 2\pi \int_(1)^(2)y√(1+64y^2)dy\\\\\\\displaystyle A = 2\pi \int_(1)^(2)√(1+64y^2)*ydy\\\\\\\displaystyle A = 2\pi \int_(65)^(257)√(u)*(du)/(128)\\\\\\`

In the last two steps I let u = 1+64y^2, so du/dy = 128y which leads to ydy = du/128.

Note the change in the limits of integration. If y = 1, then u = 1+64y^2 = 65. If y = 2, then 1+64y^2 = 257

----------------------------

Part 2

`\displaystyle A = 2\pi \int_(65)^(257)√(u)*(du)/(128)\\\\\\\displaystyle A = 2\pi*(1)/(128)\int_(65)^(257)u^(1/2)*du\\\\\\\displaystyle A = (\pi)/(64)\int_(65)^(257)u^(1/2)*du\\\\\\\displaystyle A = (\pi)/(64)\left((2)/(3)u^(3/2)+C\right)\Bigg]_(65)^(257)\\\\\\\displaystyle A = (\pi)/(64)\left(\left((2)/(3)(257)^(3/2)+C\right)-\left((2)/(3)(65)^(3/2)+C\right)\right)\\\\\\\displaystyle A = (\pi)/(64)*(2)/(3)\left((257)^(3/2)-(65)^(3/2)\right)\\\\\\`

----------------------------

Part 3

`\displaystyle A = (\pi)/(96)\left(√(257^3)-√(65^3)\right)\\\\\\\displaystyle A = (\pi)/(96)\left(√(257^2*257)-√(65^2*65)\right)\\\\\\\displaystyle A = (\pi)/(96)\left(√(257^2)*√(257)-√(65^2)*√(65)\right)\\\\\\\displaystyle A = (\pi)/(96)\left(257√(257)-65√(65)\right)\\\\\\`

`\displaystyle A = (\pi)/(96)*257√(257)-(\pi)/(96)*65√(65)\\\\\\\displaystyle A = (257\pi√(257))/(96)-(65\pi√(65))/(96)\\\\\\\displaystyle A = (-65√(65)\pi)/(96)+(257√(257)\pi)/(96)\\\\\\`