Question

9. What is the likelihood that a randomly selected couple's relationship survived between 90 and 150 days

Answer 1

0.5818

Explanation:

Suppose the average teenage romantic relationship is normally distributed with a mean number of 100 days with a standard deviation of 30 days.

Answer:

The z score is used to determine how many standard deviations that the raw score is above or below the mean. If the z score is positive then the raw score is above the mean and if it is negative then it is below the mean. It is given by:

`z=(x-\mu)/(\sigma)\\ \\where\ \mu=mean,\sigma=standard\ deviation, x=raw\ score`

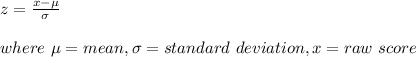
Given that:

`\mu=100\ days,\sigma=30\ days\\\\For\ x=90\\\\z=(90-100)/(30) =-0.33\\\\For\ x=150\\\\z=(150-100)/(30) =1.67`

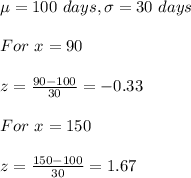
Therefore, from the normal distribution table, P(90 < x < 150) = P(-0.33 < z < 1.67) = P(z < 1.67) - P(z < -0.33) = 0.9525 - 0.3707 = 0.5818