Answer:
The proportion of individuals score at most 74 points on this test is 70%.
Explanation:
The complete question is:
Suppose that the scores on a reading ability test are normally distributed with a mean of 70 and a standard deviation of 8. What proportion of individuals score at most 74 points on this test? Round your answer to at least four decimal places.
Solution:
Let X represent the scores on a reading ability test.
It is provided that
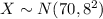 .
.
Compute the probability that an individuals score is at most 74 points on this test as follows:
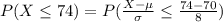
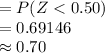
Thus, the proportion of individuals score at most 74 points on this test is 70%.