Answer:
Explanation:
Since, old figure is the dilated form of the new figure.
For the dilation of the old figure to new by a scale factor 's',
s =
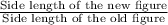 =
=
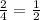
Rule for the dilation of a point by a scale factor 'k',
(x, y) → k(x, y)
→ (kx, ky)
If the vertices of the old triangle are dilated by a scale factor of
 ,
,
Coordinates of the dilated triangle of the old triangle will be,
A(3, 4) → A'(
 , 2)
, 2)
B(3, 8) → B'(
 , 4)
, 4)
C(5, 4) → C'(
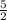 , 2)
, 2)
Now these points are rotated by an angle of 90° counterclockwise about the origin,
Rule for the rotation is,
(x, y) → (-y, x)
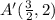 → A"(-2,
→ A"(-2,
 )
)
B'(
 , 4) → B"(-4,
, 4) → B"(-4,
C'(
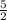 , 2) → C"(-2,
, 2) → C"(-2,
Further these points have been reflected across x-axis,
A"(-2,
 ) → P(-2, -
) → P(-2, -
 )
)
B"(-4,
 ) → Q(-4, -
) → Q(-4, -
 )
)
C"(-2,
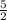 ) → R(-2, -
) → R(-2, -
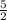 )
)
Therefore, old triangle is dilated by a scale factor of
 , followed by rotation of 90° counterclockwise about the origin and then reflected across x-axis to form the new triangle.
, followed by rotation of 90° counterclockwise about the origin and then reflected across x-axis to form the new triangle.