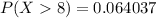Complete Question
The complete question is shown on the first uploaded image
Answer:
a
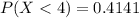
b
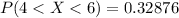
c
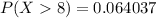
d
The correct option is B
Explanation:
From the question we are told that
The mean is
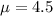
The standard deviation is
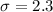
Generally the probability that a randomly selected study participant's response was less than 4 is mathematically represented as
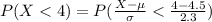
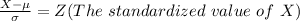
So
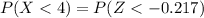
From the z-table
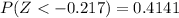
So
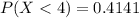
Generally the probability that a randomly selected study participant's response was between 4 and 6 is mathematically represented as
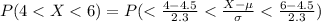
=>
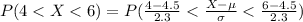
=>
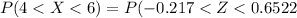
=>
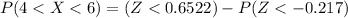
From the z-table
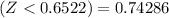
So
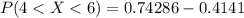
=>
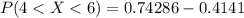
=>
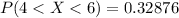
Generally the probability that a randomly selected study participant's response was more than 8 is mathematically represented as
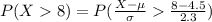
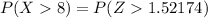
From the z-table
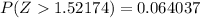
So