Question

100 Points!!!! Please HELP!!!

The Summit at Snoqualmie Ski Resort is a popular ski destination, especially with snowboarders. Last weekend, the resort had to shut down for three days because of a major storm. When the ski patrol went to check the ski paths after the blizzard, they could not find the rating signs that tell how difficult the paths are. They returned to the base lodge to check the map on the computer, but unfortunately, the storm caused a power outage. The computer that had the files listing the steepness of each path was lost. All the ski patrol could find was a scale drawing of the mountain that outlines the paths and chairlifts and show where the cabins and base lodge are. The length of each path is also on the map. John Smith, the head of the ski patrol, was not worried. He said they had all the information needed to find the steepness of each path (this would be the angle of elevation) using their trigonometry skills. The table shows three ratings for the paths.

A green circle means the path is EASY and under 30°
A blue square means the path is MODERATE and between 30° and 44°
A black diamond means the path is DIFFICULT and equal to or greater than 45°

Example: If a path has a steepness of 40°, it gets a blue square sign posted at the top of the path.

Using your trigonometric skills, calculate the steepness of each run by finding its angle of elevation. Use the space below to show your calculations and then show a summary of the results in the table. Each space on the grid represents 1 cm

Answer 1

We can use the tan trig ratio to calculate the steepness of each run.

The side opposite the angle is the vertical distance of each path.

The side adjacent to the angle is the horizontal distance of each path.

(see attached diagram)

Tan trig ratios

`\sf \tan(\theta)=(O)/(A)`

where:

• 
  `\theta` is the angle
• O is the side opposite the angle
• A is the side adjacent the angle

Little Thunder

`\implies \sf \tan(\theta)=(2)/(7)`

`\implies \sf \theta=\tan^(-1)\left((2)/(7)\right)`

`\implies \sf \theta=16^(\circ) \: (nearest\:degree)`

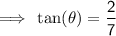
Rating = EASY (green circle)

Dodge Ridge

`\implies \sf \tan(\theta)=(4)/(6)=(2)/(3)`

`\implies \sf \theta=\tan^(-1)\left((2)/(3)\right)`

`\implies \sf \theta=34^(\circ) \: (nearest\:degree)`

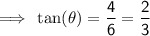
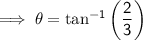
Rating = MODERATE (blue square)

Wild Side

`\implies \sf \tan(\theta)=(4)/(4)=1`

`\implies \sf \theta=\tan^(-1)(1)`

`\implies \sf \theta=45^(\circ)`

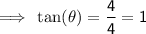
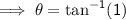
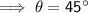
Rating = DIFFICULT (black diamond)

Pacific Crest

`\implies \sf \tan(\theta)=(4)/(8)=(1)/(2)`

`\implies \sf \theta=\tan^(-1)\left((1)/(2)\right)`

`\implies \sf \theta=27^(\circ) \: (nearest\:degree)`

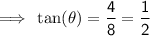
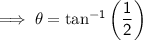
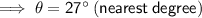
Rating = EASY (green circle)

Thunderbolt

`\implies \sf \tan(\theta)=(6)/(2)=3`

`\implies \sf \theta=\tan^(-1)(3)`

`\implies \sf \theta=72^(\circ) \: (nearest\:degree)`

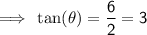
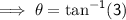
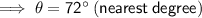
Rating = DIFFICULT (black diamond)