Question

find the point P along the directed line segment from point A(-11,1) to point B(0,-3) that divides the segment in the ratio 3 to 4

Answer 1

Hi,

See the working out on the piece of paper and don’t hesitate to ask any questions if confused!!

Answer 2

`\textsf{P}=\left(-(44)/(7),-(5)/(7)\right)`

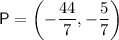
Explanation:

Given:

• A = (-11, 1)
• B = (0, -3)
• Ratio 3 : 4

Therefore, point P on the segment AB should be 3/7 of the way from point A.

`x_P=(3)/(7)(x_B-x_A)+x_A=(3)/(7)(0-(-11))-11=(-44)/(7)`

`y_P=(3)/(7)(y_B-y_A)+y_A=(3)/(7)(-3-1)+1=-(5)/(7)`

`\implies \textsf{P}=\left(-(44)/(7),-(5)/(7)\right)`

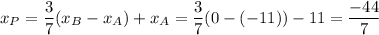
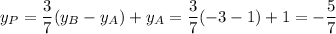
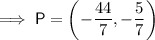
or P = (-6.3, -0.7) to 1 decimal place

(Please see attached image, where the segment AB has been divided into 7 equal parts.)