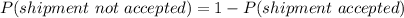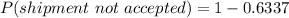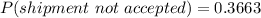Answer:
a
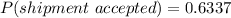 \
\
b
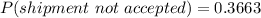
Explanation:
from the question we are told that
The number of boxes N = 100
The number of keyboard in each box is k = 20
The sample size is n = 5
Generally the number of ways of selecting 1 keyboard from the 5 selected keyboard is mathematically represented as

Here C stands for combination (Hence in the question we will be making use of the combination functionality in our calculator )
Generally the number of ways of selecting 0 keyboard from the 5 selected keyboard is mathematically represented as
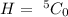
Generally the number of ways of selecting 5 keyboard from the 20 keyboards is mathematically represented as

Generally the number of ways of selecting 5 keyboard from the 15 keyboards is mathematically represented as

Generally the number of ways of selecting 5 keyboard from the 15 keyboards is mathematically represented as
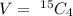
Generally the probability that a shipment will be accepted is mathematically represented as
Probability of 0 defect out of 5 + Probability of 1 defect out of 5
Now
Probability of 0 defect out of 5 is mathematically represented as
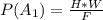
=>
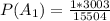
=>

And Probability of 1 defect out of 5 is mathematically represented as
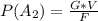
=>
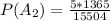
=>
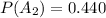
Generally the probability that a shipment will be accepted is mathematically represented as

=>
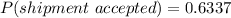
Generally the probability that this shipment will not be accepted is mathematically represented as