Question

Hizan is the owner of a company manufacturing shirts. His company is selling the shirts at a price of ₹200 per unit. The variable costs is ₹150 per unit. The fixed costs for the period is ₹5,00,000/-. Calculate the minimum number of units that must be sold for the company to attain break even. Show break even in terms of rupees.

Answer 1

Given:

Selling price = ₹200 per unit

Variable costs = ₹150 per unit.

Fixed costs for the period = ₹5,00,000

To find:

The minimum number of units that must be sold for the company to attain break even and break even in terms of rupees.

Solution:

We know that,

Total cost = Fixed cost + Variable cost

Let the number of manufacturing shirts be x, so the cost function for the shirts is

`C(x)=500000+150x`

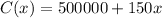
Selling price is ₹200 per unit. So, revenue function is

`R(x)=200x`

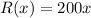
At break even point the company has no profit no loss. It means, revenue is equal to cost.

`R(x)=C(x)`

`200x=5,00,000+150x`

`200x-150x=5,00,000`

`50x=5,00,000`

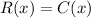
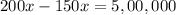
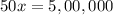
Divide both sides by 50.

`x=10000`

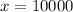
Therefore, minimum number of units that must be sold for the company to attain break even is 10,000.

To find the break even price, substitute x=10000 in either cost function or revenue function.

`R(10000)=200(10,000)`

`R(10000)=20,00,000`

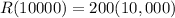
Therefore, the break even in terms of rupees is ₹20,00,000.