Question

A solid nonconducting sphere of radius R carries a charge Q distributed uniformly throughout its volume. At a certain distance rl (r (A) E/8

(B) E 78.
(C) E/2
(D) 2E
(E) 8E

Answer 1

E ’= E / 8

therefore the correct answer is A

Step-by-step explanation:

Let's calculate the electric field in an insulating sphere with a radius r <R, let's use Gauus's law, with a spherical Gaussian surface

Фi = ∫ E. dA =
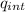`q_(int)` /ε₀

E (4πr²) = q_{int} / ε₀

density is

ρ = q_{int} / V

q_{int} = ρ V = ρ 4/3 π r³

we substitute

E (4π r²) = ρ 4/3 π r³ /ε₀

E = 1 /3ε₀ ρ r

let's change the density by

ρ = Q / V = ​​Q / (4/3 π R³)

E = 1 / 4πε₀ Q r / R³

if we now distribute the same charge on a sphere of radius R' = 2R

E ’= 1 / 4pieo Q r / (2R)³

E ’= 1 / 4ft Qr / R³ ⅛

E ’= E / 8

therefore the correct answer is A