Answer:
Allocation: 4 samples should be from the mountain and 16 from along the coast.
Explanation:
Neyman allocation is technique of sample allocation used in cases of stratified sampling.
The formula to compute the best sample size of each stratum is:
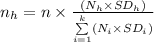
The information provided is:
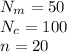
Compute the range for the number of people at the mountain campsite as follows:
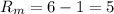
Then the standard deviation for the number of people at the mountain campsite will be:
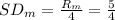
Compute the range for the number of people along the coast campsite as follows:
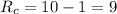
Then the standard deviation for the number of people along the coast campsite will be:
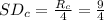
Compute the sample size for the mountain campsite as follows:
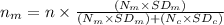
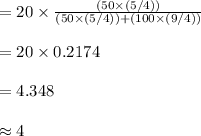
Compute the sample size for along the coast campsite as follows:
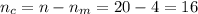
Thus, 4 samples should be from the mountain and 16 from along the coast.