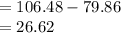Question

Un apostador pierde en su primer juego el 30% de su dinero, en el segundo juego pierde el 50% de lo que perdió; finalmente en el tercer juego pierde el 40% de todo lo que ha perdido quedándole 37 soles para seguir apostando. Dar como respuesta el dinero que el apostador tenía al principio menos su 75%

Answer 1

Responder:

26,62

Explicación paso a paso:

Sea x el dinero original que tenía el jugador:

si un jugador pierde en su primer juego el 30% de su dinero, la cantidad perdida será;

`= 30/100 \ of \ x\\= 0.3x`

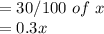
Si en el segundo juego pierde el 50% de lo que perdió, entonces la cantidad perdida en el segundo juego será:

`= 50/100 \ of \ 0.3x\\= 0.5 * 0.3x\\= 0.15x`

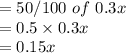
Si en el tercer juego pierde el 40% de todo lo que ha perdido, la cantidad perdida en el tercer juego será:

`=(40)/(100) \ of \ (0.3x+0.15x) \\= 0.4(0.45x)\\= 0.2025x`

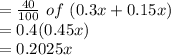
Si la cantidad que le queda para seguir apostando es de 37 soles, entonces para calcular la cantidad original que tiene, sumaremos toda la cantidad perdida y la cantidad restante y equipararemos la cantidad original x como se muestra:

0,3x + 0,15x + 0,2025x + 37 = x

0,6525x + 37 = x

x-0,6525x = 37

0,3475x = 37

x = 37 / 0,3475

x = 106,48

La cantidad que tenía originalmente era de 106,48

75% de 106,48

= 75/100 * 106,48

= 0,75 * 106,48

= 79,86

Tomando la diferencia entre su monto original y su 75% será:

`= 106.48-79.86\\= 26.62`