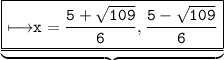
Given : A quadratic equation is given to us . The equation is 3x² - 5x - 7 = 0 .
To Find : The roots of the equation .
Solution : Given quadratic equation is 3x²-5x-7=0. So , let's factorise it to get the zeroes of the equation .
⇒ 3x² -5x - 7 = 0.
Here now , use Quadratic formula , of the quadratic equation in standard form of ax² + bx + c = 0.
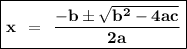
On substituting respective values ,
⇒ x = -(-5) ± √ (-5)² - 4×3×(-7) / 2 × 3.
⇒x = 5 ± √ [ 25 + 84 ]/ 6 .
⇒ x = 5 ± √ 109 / 6 .
⇒ x = 5 + √109 / 6 , 5 - √109 / 6.