s = side length of square
4s = perimeter of square
L = length of rectangle
W = width of rectangle
P = 2L+2W = perimeter of rectangle
4s = 2L+2W .... since we want the perimeters the same
4s = 2(L+W)
s = 0.5(L+W)
s^2 = (0.5(L+W))^2 ... square both sides
s^2 = 0.25(L+W)^2
The last equation shows the area of the square, s^2, in terms of L and W. This way we can connect the square to the rectangle.
-----------------------------------
The area of the rectangle is LW
Let's subtract this from the area of the square and see what we get
A = area of square = s^2
B = area of rectangle = LW
C = difference in area
C = A - B
C = s^2 - LW
C = 0.25(L+W)^2 - LW
C = 0.25(L^2+2LW+W^2) - LW
C = 0.25L^2+0.5LW+0.25W^2-LW
C = 0.25L^2-0.5LW+0.25W^2
C = 0.25(L^2-2LW+W^2)
C = 0.25(L-W)^2
Regardless of what we pick for L and W, the expression (L-W)^2 is always positive. Squaring a negative number leads to a positive result.
So C is always positive as long as
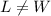
If C > 0, and C = A - B, then
C > 0
A-B > 0 .... replace C with A-B
A > B .... add B to both sides
This shows the square area is always larger than the rectangle.
Again this only works if L and W are different values. If L = W, then the argument falls apart because the rectangle becomes the square.
We make
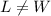 to have a nonsquare rectangle.
to have a nonsquare rectangle.