Answer:
B. They are not parallel because their slopes are not equal.
Explanation:
Find the slope of the line that runs through points (6, 3) and (-1, 5):
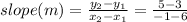
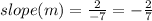
Since the slope of the line that passes through points (6, 3) and (-1, 5) is not the same with line that has a slope of ¾, therefore, both lines cannot be parallel.
The answer is "B. They are not parallel because their slopes are not equal."