Answer:
Company (1) charges $1.12 per mile and company (2) charges $0.85 per mile
Company (2) is $7.4 cheaper.
Explanation:
From the tables given in the picture,
Let the equation representing the rental 'y' and distance traveled 'x' is represented by,
y = mx + b
For company (1),
Here m = per mile rental charges = Slope of the graph
b = Initial charges
Since slope of the line passing through two points
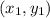 and
and
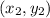 is given by,
is given by,
m =
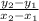
Therefore, slope of the line passing through (30, 53.55) and (60, 87.15) will be,
m =
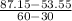 = $1.12 per mile
= $1.12 per mile
So the equation will be,
y = 1.12x + b
Since this line passes through (30, 53.55),
53.55 = 1.12(30) + b
b = 53.55 - 33.6
b = 19.95
So the expression representing charges for the company (1) will be,
y = 1.12x + 19.95
For company (2),
Per mile charges = slope of the line
m =
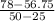
m = $0.85 per mile
Equation for the charges will be,
y = 0.85x + b
Since this line passes through (25, 56.75),
56.75 = 0.85(25) + b
b = 56.75 - 21.25
b = 35.5
Therefore, equation representing total charges for company (2) will be,
y = 0.85x + 35.5
By comparing per mile charges,
Company (1) charges $1.12 per mile and company (2) charges $0.85 per mile
Steven plans to drive 85 km in rental truck.
Charges for company (1),
y = 1.12x + 19.95
y = 1.12(85) + 19.95
y = $115.15
Charges for company (2),
y = 0.85x + 35.5
y = 0.85(85) + 35.5
y = $107.75
Difference in charges of both the companies = 115.15 - 107.75 = $7.4
Therefore, company (2) is $7.4 cheaper.