Answer:
A. No restriction on the domain of g(x); inverse is g–1(x) = RootIndex 3 StartRoot StartFraction x minus a Over 41 EndFraction EndRoot
Step-by-step explanation:
Given the function
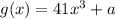 , we are to find the inverse of the function a shown below:
, we are to find the inverse of the function a shown below:
Ley y = g(x)
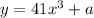
replace y with x
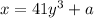
make y the subject of the formula:
![x = 41y^3+a\\41y^3 = x-a\\y^3 = (x-a)/(41) \\y = \sqrt[3]{(x-a)/(41) }](https://img.qammunity.org/2021/formulas/health/college/ngaomo8u991pi2s90g1l0dyzwta28ciimm.png)
Replace y with
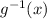
![g^(-1)(x) = \sqrt[3]{(x-a)/(41) }](https://img.qammunity.org/2021/formulas/health/college/17cbuys577yjpigw0n42oajlqqiwbaa5c6.png)
Hence the inverse function
![g^(-1)(x) = \sqrt[3]{(x-a)/(41) }](https://img.qammunity.org/2021/formulas/health/college/17cbuys577yjpigw0n42oajlqqiwbaa5c6.png)
No restriction on the domain of g(x). Hence the correct option is A