Answer:
segment AC is equal to A''B'' over 2
Step-by-step explanation:
Given that,
Scale factor = 2
The coordinates of A is (-3,3)
The coordinates of B is (1,-3)
The coordinates of C is (-3,3)
We know that, the ratio of length of new segment to the length of segment of original figure is called scale factor.
So.
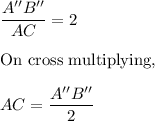
It means, segment AC is equal to A''B'' over 2 is the correct answer.