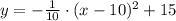Question

Tommy and Arnold are playing with water balloons. Arnold is standing by a bush that is 20 feet from where Tommy is standing. Tommy released a water balloon at 5 feet above the ground and hits Arnold’s chest- which is also 5 feet above the ground. The balloon reached a maximum height of 15 feet off the ground. using Tommy’s location as the starting point, help Tommy write an equation that describes the path of the water from the point of release to Arnold's chest. Using the equation y=a(x-h)^2+k

Answer 1

The equation that describes the path of the water balloon is:

`y =-(1)/(10)\cdot (x-10)^(2)+15`

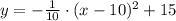
Explanation:

The motion of the water balloon is represented by quadratic functions. Tommy launches a water balloon from
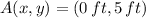`A(x,y) = (0\,ft, 5\,ft)` and hits Arnold at
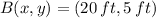`B(x,y) = (20\,ft, 5\,ft)`. Given the property of symmetry of quadratic function, water ballon reaches its maximum at
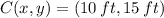`C(x,y) = (10\,ft,15\,ft)`, which corresponds to the vertex of the standard equation of the parabola, whose form is:

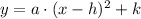`y = a\cdot (x-h)^(2)+k` (Eq. 1)

Where:

`a` - Vertex parameter, measured in
`(1)/(ft)`.

`h`,
`k` - Horizontal and vertical components of the vertex, measured in feet.

`x`,
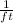`y` - Horizontal and vertical location of the ball, measured in feet.

If we know that
`x = 0\,ft`,
`y = 5\,ft`,
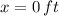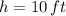`h = 10\,ft` and
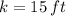`k = 15\,ft`, the vertex parameter is:

`5\,ft = a\cdot (0\,ft-10\,ft)^(2)+15\,ft`

`a = (5\,ft-15\,ft)/((0\,ft-10\,ft)^(2))`

`a = - (1)/(10)\,(1)/(ft)`

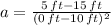
The equation that describes the path of the water balloon is:

`y =-(1)/(10)\cdot (x-10)^(2)+15`