Given:
The function is
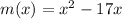
To find:
The inverse of the given function.
Solution:
We have,
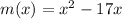
Substitute m(x)=y.
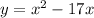
Interchange x and y.
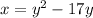
Add square of half of coefficient of y , i.e.,
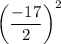 on both sides,
on both sides,
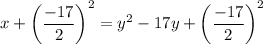
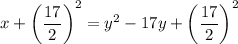
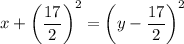
![[\because (a-b)^2=a^2-2ab+b^2]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ns8xcknd2la2h0fgcz5pt0lrf7e0cp5mva.png)
Taking square root on both sides.
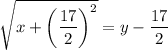
Add
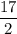 on both sides.
on both sides.
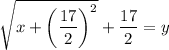
Substitute
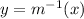 .
.
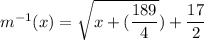
We know that, negative term inside the root is not real number. So,
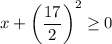
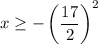
Therefore, the restricted domain is
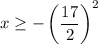 and the inverse function is
and the inverse function is
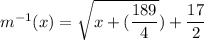 .
.
Hence, option D is correct.
Note: In all the options square of
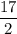 is missing in restricted domain.
is missing in restricted domain.