Question

Which statement illustrates a simulation that could be used to generate samples of people on a game show selecting either door A, door B, or door C?

A. Flipping a coin and getting heads for door A or tails for door C.

B. Rolling a die; 1 or 2 represents door A, 3 or 4 represents door B, and 5 or 6 represents door C.

C. Creating a spinner divided into 4 equal parts. Label two parts door A, one part door B, and the third part door C.

D. Go to the game show and collect data for a month on which doors people chose.

Answer 1

Its B: Rolling a die; 1 or 2 represents door A, 3 or 4 represents door B, and 5 or 6 represents door C.

Explanation:

They have to be evenly probable so its B

edge 2020

Answer 2

The correct option is;

B. Rolling a die; 1 or 2 represents door A, 3 or 4 represents door B, and 5 or 6 represents door C

Explanation:

Given that an onloaded die has equal chances of getting either 1 or 2 or 3 or 4 or 5 or 6, the chances of getting a particular score is therefore 1/6

and the probability of getting a 1 or 2 = 1/6 + 1/6 = 2/6 = 1/3

Therefore, given that the probability, P
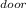`_(door)` of opening door A, or door B, or door C is the probability of selecting 1 out of 3 given as follows;

P
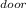`_(door)`(door A) = 1/3

P
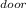`_(door)`(door B) = 1/3

P
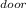`_(door)`(door C) = 1/3

Therefore, given that the probability of selecting either door A or door B or door C is equivalent to the probability of getting a 1 or 2, or a 3 or 4, or a 5 or 6 on a die.