Question

find all integers x satisfying each of the following congruences mod n. if no such x exists, explain why not

Answer 1

please find the solution:

Explanation:

please find the correct question:

Given value:

`\to 4x \equiv 2(mod\ n) \ \ \ \ \ \ \ \ \ \ \ \ _(where) \ \ n=6\\\\\to 4x \equiv 2 (mod 6)`

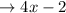`\to 4x-2` should be divisible by 6 we are also given that
`0 \leq x < n` and start with x = 0

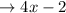`\to 4x-2` =-2 which is not divisible by 6

x= 1

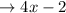`\to 4x-2` = 2 not divisilble by 6

x= 2

`\to 4x-2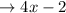` = 6 which is divisible by 6

x=3

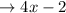`\to 4x-2` = 10 not divisible by 6

x=4

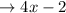`\to 4x-2` = 14 not divisible by 6

x=5

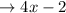`\to 4x-2` = 18 which is divisible by 6

so such x are x = 2 and x = 5