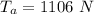Complete Question
The diagram for this question is shown on the first uploaded image
Answer:
The tension in the rope on the left of the mountain climber is
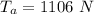
Step-by-step explanation:
From the question we are told that
The weight of the mountain climber is m = 555 N
Generally from the diagram , the total amount of force acting on the rope along the vertical axis at equilibrium is mathematically represented as
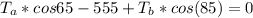
Here
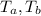 are the tension of the rope on the left and on the right hand side
are the tension of the rope on the left and on the right hand side
So

=>
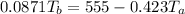
=>
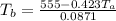
Generally from the diagram , the total amount of force acting on the rope along the horizontal axis at equilibrium is mathematically represented as
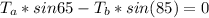
=>

=>
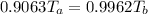
=>
![0.9063T_a = 0.9962[(555 - 0.423T_a)/(0.0871)]](https://img.qammunity.org/2021/formulas/physics/college/h6rfr0ou66cgk64dpivs6hzlqqi9o41542.png)
=>
![0.9063T_a = [(552.891 - 0.421T_a)/(0.0871)]](https://img.qammunity.org/2021/formulas/physics/college/jxc4z5q8mxhtemq2xk60hnn911u4isc4n1.png)
=>
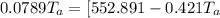
=>
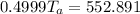
=>