Question

HELP ASAP PLSSSS

Square ABCD has vertices at A(−2, 5) and B(4, 3).

The slopes of the sides of ABCD given in simplified form are −1/3 and ?

Answer 1

The slopes of the sides of the square ABCD are -1/3 and 3

Explanation:

The coordinates of the vertices are;

A(-2, 5) and B(4, 3), therefore, we have;

The slope of segment AB, m, is given as follows;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

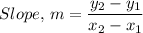
Where, (x₁, y₁) = (-2, 5) and (x₂, y₂) = (4, 3), we have;

`Slope, m \ of \ line \ AB, \ m_(AB)=(3-5)/(4-(-2)) = (-2)/(6) = -(1)/(3)`

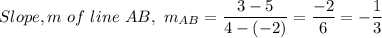
Therefore, given that the adjacent sides of a square are perpendicular, we have;

The slope of a line perpendicular to another line with slope, m is equal to the negative inverse of the slope of the line

Therefore, the given that the slope of a line = m, the slope of the perpendicular = -1/m

Therefore;

`The \ slope \ of \ the \ perpendicular \ to \ the \ line \ AB = -(1)/(The \ slope \ of \ the \ line \ AB )`

`The \ slope \ of \ the \ perpendicular \ to \ the \ line \ AB = -(1)/(-(1)/(3) ) = 3`

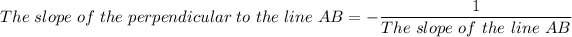
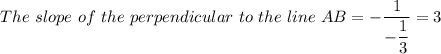
Given that the one other side is parallel to the line AB, whereby the slope of parallel lines are equal, and that two sides are perpendicular to the line AB, we have, the slopes of the sides of the square ABCD are;

-1/3 and 3.