Question

Write the equation of the line that passes through the given points.
(0,5) and (-2,-4)

Answer 1

`y=(9)/(2)x+5`

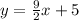
Explanation:

To find the equation of the a line that passes through the two given points, we must first find the slope between the two points. We can do this by using the slope formula. The slope formula is:

`m=(y_2-y_1)/(x_2-x_1)`

where m is the slope and (x₁, y₁) and (x₂, y₂) are two points.

By plugging in (-2, -4) and (0, 5) for (x₁, y₁) and (x₂, y₂) respectively, we get:

`y=(5-(-4))/(0-(-2))=(9)/(2)`

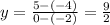
So the slope is 9/2. Now we that we have found the slope, we can write an equation. Normally, when we are given two points, we would pick one of the points and plug it into the point-slope form and then solve for slope-intercept form. Here, notice that one of the points give, (0, 5), is the y-intercept. Knowing this, we can plug in 5 for the y-intercept into the slope-intercept form to get our equation. Remember, slope-intercept form is:

y = mx + b

where m is the slope and b is the y-intercept.

Pugging in 9/2 for m and 5 for b we get:

`y=(9)/(2)x+5`

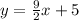
which would be our equation.

I hope this helps. Happy studying.