Question

Find the nth term of this number sequence 2, 4, 6, 8, ...​

Answer 1

`\qquad\qquad\huge\underline{{\sf Answer}}`

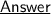
The given sequence is in Arithmetic progression, and we have to find its nth term ~

So, let's get it solved ~

First term of the sequence is :

• a = 2

Common difference is :

• d = 6 - 4 = 4 - 2 = 2

Now, if we have to write the 2nd Term with respect to first one, we can write :

• 2nd Term = a + (2 - 1)d = a + d = 2 + 2 = 4

similarly ~

• 3rd Term = a + (3 - 1)d = a + 2d = 2 + 4 = 6

• 4th Term = a + (4 - 1)d = a + 3d = 2 + 6 = 8

Therefore, I similar pattern ~

`\qquad \sf  \dashrightarrow \: nth \: term = a + (n - 1)d`

`\qquad \sf  \dashrightarrow \: nth \: term = 2 + (n - 1)2`

`\qquad \sf  \dashrightarrow \: nth \: term = 2(1 + (n - 1))`

`\qquad \sf  \dashrightarrow \: nth \: term = 2(1 + n - 1)`

`\qquad \sf  \dashrightarrow \: nth \: term = 2 n`

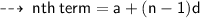
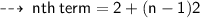
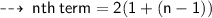
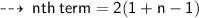
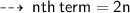
Feel free to ask your doubts, if you have any ~

Answer 2

2n

Explanation:

from the number sequence above, each term except the first is generated by adding 2 to the term immediately preceding it.

the nth term of the sequence is usually designated Tn, and it's usually a function of n

from the number sequence

T1= 2

T2 = 2+2= 4

T3= 4+2= 6

T4= 6+2= 8

therefore, Tn= 2+2×(n-1)

= 2+2n-2

=2-2+2n= 2n

therefore, the nth term of the number sequence= 2n