Question

Find a point on the ellipsoid x2+y2+4z2=36x2+y2+4z2=36 where the tangent plane is perpendicular to the line with parametric equations

Answer 1

A point on the ellipsoid is (-4,2,2) or (4,-2,-2)

Explanation:

Given equation of ellipsoid f(x,y,z) :
`x^2+y^2+4z^2=36`

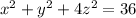
Parametric equations:

x=-4t-1

y=2t+1

z=8t+3

Finding the gradient of function

`\\abla f(x,y,z)=<\frac{\partial{f}}{\partial{x}},\frac{\partial{f}}{\partial{y}},\frac{\partial{f}}{\partial{z}}>\\\\abla f(x,y,z)=<2x,-2y,8x>`

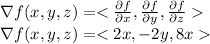
So, The directions vectors=(-4,2,8)

Now the line is perpendicular to plane when direction vector is parallel to the normal vector of line

`\\ablaf(x,y,z)=(2x,2y,8z)=\lambda(-4,2,8)`

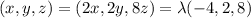
So,
`2x=-4\lambda`

`\Rightarrow x=-2\lambda`

`2y=2\lambda\\\Rightarrow y=\lambda\\8z=8\lambda\\\Rightarrow z=\lambda`

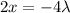
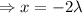
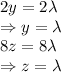
Substitute the value of x , y and z in the ellipsoid equation

`(2\lambda)^2+(\lambda)^2+4(\lambda)^2=36\\9(\lambda)^2=36\\\lambda^2=4\\\lambda=\pm 2`

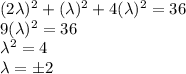
With
`\lambda = 2`

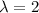
x=-2(2)=-4

y=2

z=2

With
`\lambda =- 2`

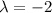
x=-2(-2)=4

y=-2

z=-2

Hence a point on the ellipsoid is (-4,2,2) or (4,-2,-2)