Question

The diagonals of a rhombus measure 8 cm by 6 cm. What is the length of a side of the rhombus?​

Answer 1

`\huge\boxed{\bf\:5\: cm}`

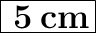
Explanation:

Let's take a rhombus with diagonals AC & BD which intersects at point E.

Take,

• AC = 8 cm
• BD = 6 cm

Now, we need to find the length of a side of a rhombus.

For this, let's take one part of the rhombus, say, △AED.

Now, since E is the midpoint of diagonals AC & BD,

• AE = AC/2 = 8/2 = 4 cm
• ED = BD/2 = 6/2 = 3 cm

AE will form the altitude & ED the base of △AED.

Then, in △AED, by following the pythagorean theorem,

Hypotenuse² = Base² + Altitude²

Hypotenuse² = 3² + 4²

Hypotenuse² = 9 + 16

Hyptenuse² = 25

Hypotenuse = √25

Hypotenuse = 5 cm

From the figure we can see that the hypotenuse of △AED forms one side of the rhombus. Since all the sides of a rhombus are equal, 5 cm is the measurement of the length of a side of the rhombus.

`\rule{150pt}{2pt}`

Please refer to the attached picture for the figure & its labelling.

`\rule{150pt}{2pt}`

Answer 2

Answer:
5 cm

Explanation:
In a rhombus,
1 diagonal = 8 cm (left - right)
2 diagonal = 6 cm (top - bottom)

There will be 4 triangles in a rhombus when bisected with 2 intersecting diagonals (all 4 will have equal measures).

Then,
Base of 1 triangle = 8/2 = 4 cm
Altitude of 2 triangle = 6/2 = 3 cm

Hypotenuse of 1 triangle = Longest side of triangle = Side of rhombus = ?

Using pythagorean property,
√((4)² + (3)²) = Hypotenuse
√(16 + 9) = Hypotenuse
√25 = Hypotenuse
5 cm = Hypotenuse = 1 side of rhombus

_______
Hope it helps ⚜