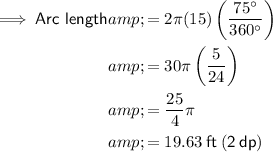Answer:
a) 19.63 ft (2 dp)
b) 147.26 ft² (2 dp)
Explanation:
To find the length of the curved fence, use the formula for arc length of a circle.
To find the area of the vegetable garden, use the formula for area of a sector of a circle.
Formula
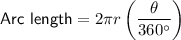
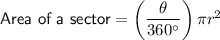
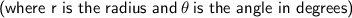
Calculation
Given:
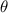 = 75°
= 75°- r = 15 ft