Question

A car at the top of a ramp starts from rest and rolls to the bottom of the ramp, achieving a certain final speed. If you instead wanted the car to achieve twice as much speed at the bottom of the ramp, how high should the ramp be compared to the first case

Answer 1

It must be 4 times high.

Step-by-step explanation:

• Assuming that the car can be treated as a point mass, and that the ramp is frictionless, the total mechanical energy must be conserved.
• This means, that at any time, the following must be true:
• ΔK (change in kinetic energy) = ΔU (change in gravitational potential energy)

⇒
`m*g*h = (1)/(2) * m*v^(2)`

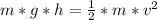
• Let's call v₁, to the final speed of the car, and h₁ to the height of the ramp.

So, at the bottom of the ramp, all the gravitational potential energy

must be equal to the kinetic energy of the car (Defining the bottom of

the ramp as our zero reference for the gravitational potential energy):

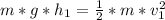`m*g*h_(1) = (1)/(2) * m*v_(1) ^(2)` (1)

• Now, let's do v₂ = 2* v₁
• Replacing in (1) we get:

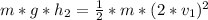`m*g*h_(2) = (1)/(2) * m*(2*v_(1)) ^(2)` (2)

• Dividing (2) by (1), and rearranging terms, we get:
• h₂ = 4* h₁