Question

An increase in temperature the kinetic energy and average speed of the gas particles. As a result, the pressure on the walls of the container . Answer Bank What temperature must a gas, initially at 10 ∘C, be brought to for the pressure to triple?

Answer 1

a

The pressure will increase

b

`T_2 =  576^oC`

Step-by-step explanation:

From the ideal gas law we have that

`PV  =  nRT`

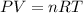
We see that the temperature varies directly with the pressure so if there is an increase in temperature that pressure will increase

The initial temperature is
`T_i  =  10^oC = 10 + 273 =  283 \  K`

The objective of this solution is to obtain the temperature of the gas where the pressure is tripled

Now from the above equation given that nR and V are constant we have that

`(P)/(T)  =  constant`

=>
`(P_1)/(T_1)  =(P_2)/(T_2)`

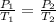
Let assume the initial pressure is
`P_1 =  1 Pa`

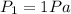
So tripling it will result to the pressure being
`P_2 =  3 Pa`

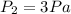
So

`(1)/(283)  =(3)/(T_2)`

=>
`T_2  =  3 *  283`

=>
`T_2  =  3 *  283`

=>
`T_2  = 849 \ K`

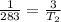
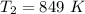
Converting back to
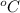
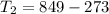
`^oC`

`T_2  =  849 -  273`

=>
`T_2 =  576^oC`