Question

If you roll two six-faced dice together, you will get 36 possible outcomes. 4 pts 1. List all possible outcomes of the experiment. 2 pts 2. What is the probability of getting a sum of 11 in these outcomes? 2 pts 3. What is the probability of getting a sum less than or equal to 4? 2 pts 4. What is the probability of getting a sum of 13 or more?

Answer 1

Given:

Two dice are rolled together.

Total number of possible outcomes.

To find:

The list of total possible outcomes.

The probability of getting a sum of 11 in these outcomes.

The probability of getting a sum less than or equal to 4.

The probability of getting a sum of 13 or more.

Solution:

If two dice are rolled together, then the total number of possible outcomes is 36 and list of total possible outcomes is

S = {(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}

Sum of 11 in these outcomes = {(5,6),(6,5),(6,6)} = 3

The probability of getting a sum of 11 in these outcomes is

`P(\text{sum=11})=(3)/(36)`

`P(\text{sum=11})=(1)/(12)`

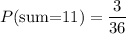
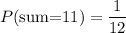
Therefore, the probability of getting a sum of 11 in these outcomes is
`(1)/(12)`.

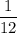Sum less than or equal to 4 = {(1,1),(1,2),(1,3),(2,1),(2,2),(3,1)} = 6

The probability of getting a sum less than or equal to 4 is

`P({sum\leq 4})=(6)/(36)`

`P({sum\leq 4})=(1)/(6)`

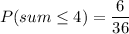
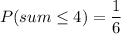
Therefore, the probability of getting a sum less than or equal to 4 is
`(1)/(6)`.

Sum of 13 or more = empty set because maximum sum is 12.

The probability of getting a sum of 13 or more is

`P(sum\geq 13)=(0)/(36)`

`P({sum\geq 13})=0`

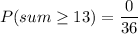
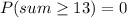
Therefore, the probability of getting a sum of 13 or more is 0.