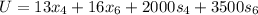Question

Suppose a certain manufacturing company produces connecting rods for 4- and 6-cylinder automobile engines using the same production line. The cost required to set up the production line to produce the 4-cylinder connecting rods is $2,100, and the cost required to set up the production line for the 6-cylinder connecting rods is $3,500. Manufacturing costs are $13 for each 4-cylinder connecting rod and $16 for each 6-cylinder connecting rod. Hawkins makes a decision at the end of each week as to which product will be manufactured the following week. If a production changeover is necessary from one week to the next, the weekend is used to reconfigure the production line. Once the line has been set up, the weekly production capacities are 5,000 6-cylinder connecting rods and 8,000 4-cylinder connecting rods. Let

x4 = the number of 4-cylinder connecting rods produced next week
x6 = the number of 6-cylinder connecting rods produced next week
s4 = 1 if the production line is set up to produce the 4-cylinder connecting rods; 0 if otherwise
s6 = 1 if the production line is set up to produce the 6-cylinder connecting rods; 0 if otherwise

Required:
Using the decision variables x4 and s4, write a constraint that sets next week.

Answer 1

Generally the constraint that sets next week are shown below

Generally the constrain that sets next week maximum production of connecting rod for 4 cylinder to W_4 or 0 is

`x_4 \le W_4 *  s_4`

`x_4 \le 5000 *  s_4`

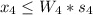
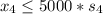
Generally the constrain that sets next week maximum production of connecting rod for 6 cylinder to W_6 or 0 is

`x_6 \le W_6 *  s_6`

`x_6 \le 8,000 *  s_6`

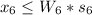
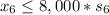
Generally the constrain that limits the production of connecting rods for both 4 cylinder and 6 cylinders is

`x_4 \le W_4 *  s_6`

=>
`x_4 \le 5000 *  s_6`

`x_4 \le W_6 *  s_4`

=>
`x_4 \le 8000 *  s_4`

`s_4 + s_6 = 1`

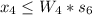
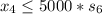
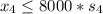
The minimum cost of production for next week is

`U  =  M_4 *  x_4 + M_6 * x_6 + C_4 * s_4 + C_6 * s_6`

=>
`U  =  13x_4 + 16x_6 + 2000 s_4 + 3500 s_6`

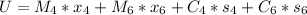
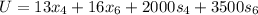
Explanation:

The cost for the four cylinder production line is
`C_4 =  \$2,100`

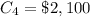
The cost for the six cylinder production line is
`C_6 = \$3,500`

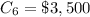
The manufacturing cost for each four cylinder is
`M_4= \$13`

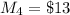
The manufacturing cost for each six cylinder is
`M_6= \$16`

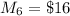
The weekly production capacity for 4 cylinder connecting rod is
`W_4 = 5,000`

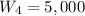
The weekly production capacity for 6 cylinder connecting rod is
`W_6 = 8,000`

Generally the constraint that sets next week are shown below

Generally the constrain that sets next week maximum production of connecting rod for 4 cylinder to W_4 or 0 is

`x_4 \le W_4 *  s_4`

`x_4 \le 5000 *  s_4`

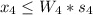
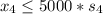
Generally the constrain that sets next week maximum production of connecting rod for 6 cylinder to W_6 or 0 is

`x_6 \le W_6 *  s_6`

`x_6 \le 8,000 *  s_6`

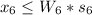
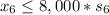
Generally the constrain that limits the production of connecting rods for both 4 cylinder and 6 cylinders is

`x_4 \le W_4 *  s_6`

=>
`x_4 \le 5000 *  s_6`

`x_4 \le W_6 *  s_4`

=>
`x_4 \le 8000 *  s_4`

`s_4 + s_6 = 1`

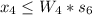
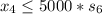
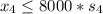
The minimum cost of production for next week is

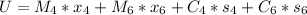
`U  =  M_4 *  x_4 + M_6 * x_6 + C_4 * s_4 + C_6 * s_6`

=>
`U  =  13x_4 + 16x_6 + 2000 s_4 + 3500 s_6`