Answer:
a) 7.14e19 Hz
b) 2.298e-27 J
c) 2.793e-19 J; 7.117e9 nm
d) 7.5e14 Hz; 4.96e-19 J
e) 6.2947e-18 J; 31.6 nm
f) 2.21e-22 J
g) 7.1e-19 J; 1.1e15 Hz
h) 3.422e-19 J; 581 nm
i) 4.2e14 Hz
j) 1.92e8 m
k) 7.14e16 Hz; Ultraviolet
Step-by-step explanation:
Frequency: ν Wavelength: λ Energy: E Speed of light: C (3.00e8) Planck's Constant: h (6.626e-34)
ν -> λ λ = C/ν
λ -> ν ν = C/λ
For either of these equations, wavelength must be converted to meters or nanometers, depending on the equation.
For ν -> λ, after doing the equation, convert the wavelength into nanometers by dividing by 1e-9.
For converting λ -> ν, convert the wavelength into meters by multiplying by 1e-9.
For energy: E = hν = hc/λ
Now that the setup is out of the way:
a) Violet light has a wavelength of 4.20 x 10-12 m. What is the frequency?
λ -> ν ν = C/λ
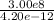 = 7.14e19 Hz
= 7.14e19 Hz
b) A photon has a frequency (n) of 3.468 x 106 Hz. Calculate its energy
E = hν = hc/λ
(6.626e-34) (3.468e6) = 2.298e-27 J
c) Calculate the energy (E) and wavelength (l) of a photon of light with a frequency of 4.215 x 1014 Hz.
E = hν = hc/λ
(6.626e-34) (4.215e14) = 2.793e-19 J
ν -> λ λ = C/ν
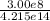 = 7.117 m
= 7.117 m
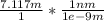 = 7.117e9 nm
= 7.117e9 nm
d) Calculate the frequency and the energy of blue light that has a wavelength of 400 nm (h = 6.62 x 10-34 J-s).
λ -> ν ν = C/λ
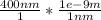 = 4e-7 m
= 4e-7 m
 = 7.5e14 Hz
= 7.5e14 Hz
E = hν = hc/λ
(6.626e-34) (7.5e14) = 4.96e-19 J
e) Calculate the wavelength and energy of light that has a frequency of 9.5 x 1015 Hz.
ν -> λ λ = C/ν
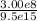 = 3.16e-8 m
= 3.16e-8 m
 = 31.6 nm
= 31.6 nm
E = hν = hc/λ
(6.626e-34) (9.5e15) = 6.2947e-18 J
f) A photon of light has a wavelength of 0.090 cm. Calculate its energy.
E = hν = hc/λ
Convert the wavelength from cm to meters:
 = 9e-4 m
= 9e-4 m
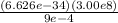 = 2.21e-22 J
= 2.21e-22 J
g) Calculate the energy and frequency of red light having a wavelength of 2.80 x 10-5 cm.
E = hν = hc/λ
Convert the wavelength from cm to meters:
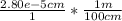 = 2.8e-7 m
= 2.8e-7 m
 = 7.1e-19 J
= 7.1e-19 J
λ -> ν ν = C/λ
Convert the wavelength from cm to meters:
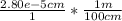 = 2.8e-7 m
= 2.8e-7 m
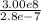 = 1.1e15 Hz
= 1.1e15 Hz
h) Calculate the energy (E) and wavelength (l) of a photon of light with a frequency of 5.165 x 1014 Hz.
E = hν = hc/λ
(6.626e-34) (5.165e14) = 3.422e-19 J
ν -> λ λ = C/ν
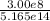 = 5.81e-7 m
= 5.81e-7 m
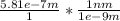 = 581 nm
= 581 nm
i) The wavelength of green light from a traffic signal is centered at 7.20 x 10-5 cm. Calculate the frequency.
λ -> ν ν = C/λ
Convert the wavelength from cm to meters:
 = 7.2e-7 m
= 7.2e-7 m
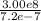 = 4.2e14 Hz
= 4.2e14 Hz
j) If it takes 1.56 seconds for radio waves (which travel at the speed of light) to reach the moon from Earth, how far away is the moon?
All we want to do here is to convert frequency (speed) to wavelength (distance). This problem requires a bit of thought, but it isn't bad once you realize that frquency is speed and wavelength is distance. It becomes just like the other problems after that. Also, I'll leave this distance in meters, but I think you can figure out how to convert it if it wants it in another unit.
One second is equal to 1 Hertz, so our frequency is 1.56 Hz.
ν -> λ λ = C/ν
 = 1.92e8 m
= 1.92e8 m
The actual distance from the earth to the moon via google is 3.84e7, but sometimes problems like this will mess with the numbers to make sure that you didn't just look up the answer. I'm still pretty sure that this is right, however.
k) Calculate the frequency of light that has a wavelength of 4.20 x 10-9m. Identify the type of electromagnetic radiation.
First, we convert wavelength to frequency, as normal:
λ -> ν ν = C/λ
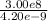 = 7.14e16 Hz
= 7.14e16 Hz
Then we identify the electromagnetic wave type. You can look up a conversion chart for these on google, but since our frequency is in the e15 - e17 range, this light is considered ultraviolet.