Question

Use the definition of continuity and the properties of limits to show that the function f(x) = x^2-9/(x^2-x-6)(x^2+6x+9) is continuous at x=2

Answer 1

See below

Explanation:

Factor the numerator and denominator

`\displaystyle f(x)=(x^2-9)/((x^2-x-6)(x^2+6x+9))\\\\f(x)=((x+3)(x-3))/((x-3)(x+2)(x+3)(x+3))\\\\f(x)=(x-3)/((x-3)(x+2)(x+3))`

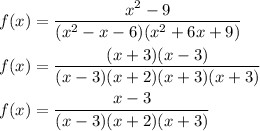
Because
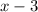`x-3` exists in both the numerator and denominator, there will be a hole at
`x=3` because the function is not continuous at that point.

If we check if the function is continuous at
`x=2`, we can see that the denominator will not be 0, thus, the function is continuous at
`x=2`.