Question

Which of the following scenarios is possible for the resultant velocity of an airplane in a strong wind to be 150 m/s?

A. The wind is blowing at 10 m/s. The airplane is flying against the wind at 140 m/s.

B. The wind is blowing at 20 m/s. The airplane is flying with the wind at 130 m/s.

C. The wind is blowing at 200 m/s. The airplane is flying with the wind at 50 m/s.

D. The wind is blowing at 50 m/s. The airplane is flying against the wind at 100 m/s.​

Answer 1

B. The wind is blowing at 20 m/s. The airplane is flying with the wind at 130 m/s.

Step-by-step explanation:

Answer 2

B. The wind is blowing at 20 m/s. The airplane is flying with the wind at 130 m/s.

Step-by-step explanation:

From Physics we get that resultant velocity of an airplane is the sum of an absolute velocity and a relative velocity, that is:

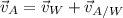`\vec v_(A) = \vec v_(W)+\vec v_(A/W)` (Eq. 1)

Where:

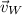`\vec v_(W)` - Wind velocity, measured in meters per second.

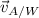`\vec v_(A/W)` - Airplance velocity relative to wind, measured in meters per second.

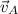`\vec v_(A)` - Airplane velocity, measured in meters per second.

If we assume that
`\vec v_(W) = 20\,\hat{i}\,\,\,\left[(m)/(s) \right]` (The airplane flies with the wind),
`\vec v_(A/W) = 130\,\hat{i}\,\,\,\left[(m)/(s) \right]`, then the resultant velocity of the airplane is:

`\vec v_(A) = 20\,\hat{i}+130\,\hat{i}\,\,\,\left[(m)/(s) \right]`

`\vec v_(A) = 150\,\hat{i}\,\,\,\left[(m)/(s) \right]`

Therefore, correct answer is B.