Question

A company is approached by a new warehouse management systems vendor to adopt a new system. The vendor claims that the warehouse management system reduces the average pick, pack, and ship time to below 3 minutes per order through bin location and routing optimization. You are given an opportunity visit an existing customer of the vendor. The customer allowed you to collect data for further analysis. You performed a time study and collected data about pick, pack ship duration of 25 shipments. Given, the data in the attached excel sheet

(Q1) perform a hypothesis testing by Use alpha=0.05 for hypothesis testing.
a. Stating your null and alternate hypotheses
b. Perform the proper hypothesis test and discuss your assessment of the vendor's claim.

Answer 1

a

The null hypothesis is
`H_o  :  \mu  = 180`

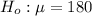
The alternative hypothesis is
`H_a :  \mu  <  180`

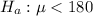
b

The decision rule is fail to reject the null hypothesis

The conclusion

There no sufficient evidence to support the vendor claim that the warehouse management system reduces the average pick, pack, and ship time to below 3 minutes(180 seconds) per order through bin location and routing optimization

Explanation:

From the question we are told that

The population mean is
`\mu  =  3 \  minutes =  180 \  seconds`

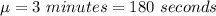
The sample size is n = 25

The excel sheet is show on the first uploaded image

The level of significance is
`\alpha =  0.05`

The null hypothesis is
`H_o  :  \mu  = 180`

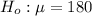
The alternative hypothesis is
`H_a :  \mu  <  180`

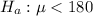
Generally the sample mean is mathematically represented as

`\= x  =  (156 + 136 + \cdots  + 181)/(25)`

=>
`\= x  = 173.2`

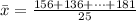
Generally the standard deviation is mathematically represented as

`\sigma  =  \sqrt{(\sum  (x_i - \= x )^2 )/(n) }`

=>
`\sigma  =  \sqrt{(  (156 - 173.2 )^2 + (136 - 173.2 )^2  + \cdots + (181- 173.2 )^2  )/(25) }`

=>
`\sigma  =  24.261`

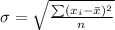
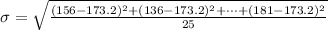
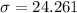
Generally the test statistics is mathematically represented as

`t =  (\= x  -  \mu )/((\sigma)/(√(n) ) )`

=>
`t =  (173.2 -  180 )/((24.261)/(√(25) ) )`

=>
`z = -1.40`

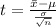
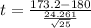
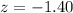
Generally p-value is mathematically represented as

`p-value  =  P(Z <  z)`

=>
`p-value  =  P(Z < -1.40)`

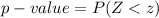
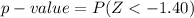
From the z-table

`P(Z < -1.40) =  0.080757`

=>
`p-value  = 0.080757`

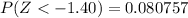
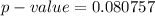
From the obtained value we that
`p-value >  \alpha`

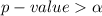
The decision rule is fail to reject the null hypothesis

The conclusion

There no sufficient evidence to support the vendor claim that the warehouse management system reduces the average pick, pack, and ship time to below 3 minutes(180 seconds) per order through bin location and routing optimization