Question

In the adjoining figure , AB = 6 , BC = 8 ,
`\angle` ABC = 90° , BD ⊥ AC and
`\angle` ABD =
`\theta` , find the value of sin
`\theta`.

Answer 1

Here we are given with a triangle with smaller triangles formed due to the altitude on AC. Given:

• AB = 6
• BC = 8
• <ABC = 90°
• BD ⊥ AC
• <ABD =
  `\theta`

We have to find the value for sin
`\theta`

So, Let's start solving....

In ∆ADB and ∆ABC,

• <A = <A (common)
• <ABC = <ADB (90°)

So, ∆ADB ~ ∆ABC (By AA similarity)

The corresponding sides will be:

`\sf{ (AD)/(AB) = (AB)/(AC) }`

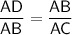
We know the value of AB and to find AC, we can use Pythagoras theoram that is:

AC = √6² + 8²

AC = 10

Coming back to the relation,

`\sf{ (AD)/(6) = (6)/(10) }`

`\sf{AD = (6 * 6)/(10) = 3.6}`

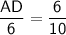
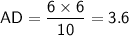
In ∆ADB, we have to find sin
`\theta` which is given by perpendicular/base:

`\sf{\sin( \theta) = (AD)/(AB) }`

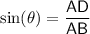
Plugging the values of AD and AB,

`\sf{\sin( \theta) = (3.6)/(6) }`

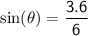
Simplifying,

`\sf{ \sin( \theta) = (3)/(5) = \boxed{ \red{0.6}}}`

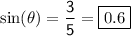
And this is our final answer.....

Carry On Learning !