Question

A market researcher for a consumer electronics company wants to determine if the residents of a particular city are spending more time watching TV than the average for this geographic area. The average for this geographic area is 13 hours per week. A random sample of 16 respondents of the city is selected, and each respondent is instructed to keep a detailed record of all television viewing in a particular week. For this sample the viewing time per week has a mean of 15.3 hours and a sample standard deviation sn = 3.8 hours. Assume that the amount of time of television viewing per week is normally distributed. Can the researcher claim that the residents of this particular city are spending significantly (at 5% level) more time watching TV than the average for this geographic area? Explain your conclusion.

Answer 1

The conclusion

There is sufficient evidence to conclude that the the residents of this particular city are spending significantly (at 5% level) more time watching TV than the average for this geographic area.

Explanation:

From the question we are told that

The population mean is
`\mu = 13 \ hours\ per\ week`

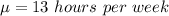
The sample size is n= 16

The sample mean is
`\= x = 15.3`

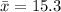
The standard deviation is
`s = 3.8\ hours.`

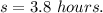
The null hypothesis is
`H_o : \mu = 13`

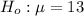
The alternative hypothesis is
`H_a : \mu > 13`

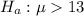
The level of significance is
`\alpha = 0.05`

Generally the test statistics is mathematically represented as

`t = (\= x - \mu )/( (\sigma )/(√(n) ) )`

=>
`t = (15.3 - 13 )/( ( 3.8 )/(√(16) ) )`

=>
`t = 2.42`

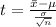
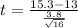
Generally the p-value is mathematically represented as

`p-value = P(z > 2.42)`

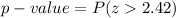
From the z -table

`P(z > 2.42) = 0.0077603`

=>
`p-value = 0.0077603`

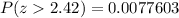
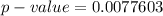
From the values obtained we see that
`p-value < \alpha`

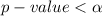
Hence we reject the null hypothesis

Therefore there is sufficient evidence to conclude that the the residents of this particular city are spending significantly (at 5% level) more time watching TV than the average for this geographic area.