Complete Question
The complete question is shown on the first and second uploaded image
Answer:
The correct option is the first and the last option
Explanation:
From the question we are told that
The sample size is n = 10
The null hypothesis is
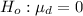
The alternative hypothesis is
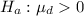
The test statistics is
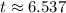
The level of significance is

Generally the p-value is mathematically represented as

From z-table
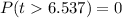
So
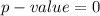
From the value obtained we see that
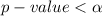 hence we reject the null hypothesis that the true mean difference between the number of units sold after the billboard was placed and the number of units sold before the billboard was placed is equal to zero
hence we reject the null hypothesis that the true mean difference between the number of units sold after the billboard was placed and the number of units sold before the billboard was placed is equal to zero
Thus we conclude that
Based on the results of the hypothesis test, there is not enough evidence at the level of significance(0.05) to suggest that the true mean difference between the number of units sold after the billboard was placed and the number of units sold before the billboard was placed is greater than zero