Question

So far, Ricardo has scores of 13, 17, 19 and 21 points for the first four rounds of a dice game. What does he need the total score to be for the next two rounds combined in order to achieve an average score of 20 points per round for all six rounds?

Answer 1

40 points

Explanation:

The score for the first four rounds of the game is 13, 17, 19, and 21 points.

Let
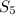`S_5` and
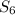`S_6` be the scores of the fifth and sixth games respectively in order to achieve an average score of 20 points per round for all six rounds.

`\text{Average score} = \frac{\text{Sum of the scores of all the rounds}}{\text{Total number of the rounds}}`

`\Rightarrow 20=(13+17+19+21+S_5+S_6)/(6)`

`\Rightarrow 20*6=80+S_5+S_6`

`\Rightarrow S_5+S_6=120-80=40.`

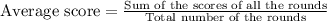
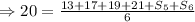
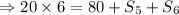
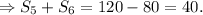
Hence, the combined score of the fifth and sixth rounds are 40 points.