Question

The number of tickets sold each day for an upcoming performance is given by p(x) = -0.4x2 + 8.8x + 13, where x is the number of days since the concert was first announced. When will daily ticket sales peak and how many tickets will be sold that day?

Answer 1

The maximum sale of the tickets is 158 on the
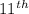`11^(th)` day.

Explanation:

The number of tickets sold each day, p(x), for an upcoming performance is

`p(x)=-0.4x^2+8.8x+13`

where x is the number of days since the concert was first announced.

For peak sales, the point of maxima has to be determined.

So, differentiate the function of the number of tickets sold each day, p(x), with respect to the number of days, x, and equate it to zero to get the extremum point (maxima or minima), i.e.

`\frac {p(x)}{dx}=0`

`\Rightarrow -0.8x+8.8=0`

`\Rightarrow x=(8.8)/(0.8)=11`

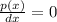
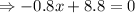
Now, check the sign of the second derivative at x=11, to ensure the obtained point is corresponding to the maxima or minima,

`\frac {p^2(x)}{dx^2}=-0.8`

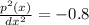
As the second derivative is negative, so x=11 is the point corresponding to maxima.

Hence, on the
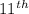`11^(th)` day the daily ticket sales will be at the peak.

Putting x=11 in the function p(x) to get the number of tickets sold that day.

`p(x=11)= -0.4(11)^2+8.8(11)+13`

`\Rightarrow 158.2.`

The number of tickets should be an integer, the obtained peak value is 158.2 so the higher integral value is not possible but the lower integral value is possible.

So, the maximum sale of the tickets is 158 on the
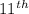`11^(th)` day.