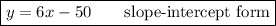Question

Consider a line whose slope is 6 and which passes through the point (8.–2).

3. Write the equation of the
4. Write the equation of the
line in point-slope form.
line in slope-intercept form.

Answer 1

`y=6(x-8)-2\qquad\text{point-slope form}`

`y=6x-50\qquad\text{slope-intercept form}`

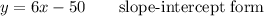
Explanation:

The equation of a line can be written in several forms. Two of the most-used forms are the point-slope and the slope-intercept forms.

The point-slope form requires to have one point (xo, yo) through which the line passes and the slope m. The equation expressed in this form is:

`y=m(x-xo)+yo`

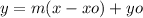
The slope-intercept form requires to have the slope m and the y-intercept b, or the y-coordinate of the point where the line crosses the y-axis. The equation is:

`y=mx+b`

The line considered in the question has a slope m=6 and passes through the point (8,-2). These data is enough to find the point-slope form of the line:

`\boxed{y=6(x-8)-2\qquad\text{point-slope form}}`

To find the slope-intercept form, we operate the above equation:

`y=6x-48-2`

`\boxed{y=6x-50\qquad\text{slope-intercept form}}`