Question

An analyst wants to determine if there is any difference in the amount of time teenagers play video games between two years. To do this, he takes a random sample of teenagers and gathers the average time they spent playing video games the previous year and compares it to the average time they spent playing video games this year. Suppose that data were collected for a random sample of 15 teenagers, where each difference is calculated by subtracting the time spent playing video games this year from the time spent playing video games last year. Assume that the times are normally distributed. What is/are the critical value(s) of the t-test statistic for this hypothesis test, where α=0.10? Use a comma and a space to separate answers as needed.

Answer 1

The critical value is
`t_{(0.10)/(2) , 14 } =[ - 1.761,1.761]`

Explanation:

From the question we are told that

The sample size is n = 15

The level of significance is
`\alpha = 0.10`

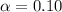
The null hypothesis is
`H_o : \mu _1 = \mu_2`

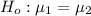
The alternative hypothesis is
`H_a : \mu_1 \\e \mu_2`

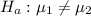
Here
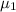`\mu_1` is average time for previous year

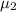`\mu_2` is the average time for current year

Generally the degree of freedom is mathematically represented as

`df = n -1`

=>
`df = 15 - 1`

=>
`df = 14`

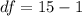
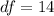
Generally from the student t distribution table the critical value for
`(\alpha )/(2)` at a degree of freedom of
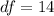`df = 14` for a two tailed test is

`t_{(0.10)/(2) , 14 } =[ - 1.761,1.761]`