Question

In a recent study on world​ happiness, participants were asked to evaluate their current lives on a scale from 0 to​ 10, where 0 represents the worst possible life and 10 represents the best possible life. The mean response was with a standard deviation of . ​(a) What response represents the ​percentile? ​(b) What response represents the ​percentile? ​(c) What response represents the ​quartile? ​(a) The response that represents the percentile is nothing. ​(Round to two decimal places as​ needed.) ​(b) The response that represents the percentile is nothing. ​(Round to two decimal places as​ needed.) ​(c) The response that represents the quartile is nothing. ​(Round to two decimal places as​ needed.)

Answer 1

(a) 8.35

(b) 5.98

(c) 3.86

Explanation:

The complete question is:

In a recent study on world​ happiness, participants were asked to evaluate their current lives on a scale from 0 to​ 10, where 0 represents the worst possible life and 10 represents the best possible life. The mean response was 5.4 with a standard deviation of 2.3. ​(a) What response represents the 90th ​percentile? ​(b) What response represents the ​60th percentile? ​(c) What response represents the ​first quartile? ​

Solution:

Assume that the world​ happiness ratings follows a Normal distribution with parameters μ = 5.4 and σ = 2.3.

(a)

Compute the response representing the 90th ​percentile as follows:

P (X < x) = 0.90

⇒ P (Z < z) = 0.90

The value of z for the above probability is, z = 1.282.

Compute the value of x as follows:

`x=\mu+z\sigma`

`=5.4+(1.282* 2.3)\\\\=5.4+2.9486\\\\=8.3486\\\\\approx 8.35`

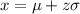
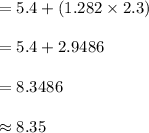
Thus, the response representing the 90th ​percentile is 8.35.

(b)

Compute the response representing the 60th ​percentile as follows:

P (X < x) = 0.60

⇒ P (Z < z) = 0.60

The value of z for the above probability is, z = 0.25.

Compute the value of x as follows:

`x=\mu+z\sigma`

`=5.4+(0.25* 2.3)\\\\=5.4+0.575\\\\=5.975\\\\\approx 5.98`

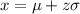
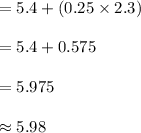
Thus, the response representing the 60th ​percentile is 5.98.

(c)

Compute the response representing the first quartile of the 25th percentile as follows:

P (X < x) = 0.25

⇒ P (Z < z) = 0.25

The value of z for the above probability is, z = -0.67.

Compute the value of x as follows:

`x=\mu+z\sigma`

`=5.4+(-0.67* 2.3)\\\\=5.4-1.541\\\\=3.859\\\\\approx 3.86`

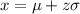
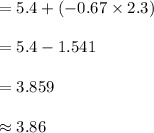
Thus, the response representing the first quartile is 3.86.