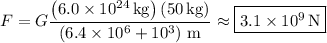Question

Please help. Its due tomorrow. I’m not really surr what to do.

Answer 1

The gravitational force F between two bodies of respective masses M and m and distance R is

`F = G(Mm)/(R^2)`

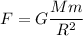
where G ≈ 6.7 × 10⁻¹¹ m³/(kg•s) is the universal gravitational constant.

8.1.1. Let M = mass of Earth, m = mass of person, and R = radius of Earth. At point C, the distance between the center of the Earth and the person is 3R, so the gravitational force has magnitude

`F = G \frac{\left(6.0*10^(24)\,\mathrm{kg}\right) \left(50\,\mathrm{kg}\right)}{3*6.4*10^6\,\mathrm m} \approx \boxed{1.0*10^9 \,\mathrm{N}}`

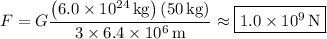
8.1.2. Using the same values for M and m, now take R = radius of Earth + 10³ m. Then the gravitational force is

`F = G \frac{\left(6.0*10^(24)\,\mathrm{kg}\right) \left(50\,\mathrm{kg}\right)}{\left(6.4*10^6+10^3\right)\,\mathrm m} \approx \boxed{3.1*10^9 \,\mathrm{N}}`